[프로그래머스/JAVA] 동굴 탐험
[본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]

오지 탐험가인 프로도는 탐험 도중 n개의 방으로 이루어진 지하 동굴을 탐험하게 되었습니다. 모든 방에는 0부터 n - 1 까지 번호가 붙어있고, 이 동굴에 들어갈 수 있는 유일한 입구는 0번 방과 연결되어 있습니다. 각 방들은 양방향으로 통행이 가능한 통로로 서로 연결되어 있는데, 서로 다른 두 방을 직접 연결하는 통로는 오직 하나입니다. 임의의 서로 다른 두 방 사이의 최단경로는 딱 한 가지만 있으며, 또한 임의의 두 방 사이에 이동이 불가능한 경우는 없습니다.
탐험에 앞서 이 지하 동굴의 지도를 손에 넣은 프로도는 다음과 같이 탐험 계획을 세웠습니다.
- 모든 방을 적어도 한 번은 방문해야 합니다.
- 특정 방은 방문하기 전에 반드시 먼저 방문할 방이 정해져 있습니다. 2-1. 이는 A번 방은 방문하기 전에 반드시 B번 방을 먼저 방문해야 한다는 의미입니다. 2-2. 어떤 방을 방문하기 위해 반드시 먼저 방문해야 하는 방은 없거나 또는 1개 입니다. 2-3. 서로 다른 두 개 이상의 방에 대해 먼저 방문해야 하는 방이 같은 경우는 없습니다. 2-4. 어떤 방이 먼저 방문해야 하는 방이면서 동시에 나중에 방문해야 되는 방인 경우는 없습니다.
위 계획 중 2-2, 2-3, 2-4는 순서를 지켜 방문해야 하는 두 방의 쌍이 A → B(A를 먼저 방문하고 B를 방문함) 형태로 유일함을 의미합니다. 즉, 프로도는 아래와 같은 형태로 방문순서가 잡히지 않도록 방문 계획을 세웠습니다.
A → B, A → C(방문순서 배열 order = [...,[A,B],...,[A,C],...]) 형태로 A를 방문 후에 방문해야 할 방이 B와 C로 두 개 또는 그 이상인 경우X → A, Z → A(방문순서 배열 order = [...,[X,A],...,[Z,A],...]) 형태로 A를 방문하기 전에 방문해야 할 방이 X와 Z로 두 개 또는 그 이상 인 경우A → B → C(방문순서 배열 order = [...,[A,B],...,[B,C],...) 형태로 B처럼 A 방문 후이면서 동시에 C 방문 전인 경우
그리고 먼저 방문해야 할 방과 나중에 방문할 방을 반드시 연속해서 방문해야 할 필요는 없어 A방을 방문한 후 다른 방을 방문한 후 B방을 방문해도 좋습니다.
방 개수 n, 동굴의 각 통로들이 연결하는 두 방의 번호가 담긴 2차원 배열 path, 프로도가 정한 방문 순서가 담긴 2차원 배열 order가 매개변수로 주어질 때, 프로도가 규칙에 맞게 모든 방을 탐험할 수 있을 지 return 하도록 solution 함수를 완성해주세요.
[제한사항]
- n은 2 이상 200,000 이하입니다.
- path 배열의 세로(행) 길이는 n - 1 입니다.
- path 배열의 원소는 [방 번호 A, 방 번호 B] 형태입니다.
- 두 방 A, B사이를 연결하는 통로를 나타냅니다.
- 통로가 연결하는 두 방 번호가 순서없이 들어있음에 주의하세요.
- order 배열의 세로(행) 길이는 1 이상 (n / 2) 이하입니다.
- order 배열의 원소는 [방 번호 A, 방 번호 B] 형태입니다.
- A번 방을 먼저 방문한 후 B번 방을 방문해야 함을 나타냅니다.
입출력 예
| n | path | order | result |
|---|---|---|---|
| 9 | [[0,1],[0,3],[0,7],[8,1],[3,6],[1,2],[4,7],[7,5]] | [[8,5],[6,7],[4,1]] | true |
| 9 | [[8,1],[0,1],[1,2],[0,7],[4,7],[0,3],[7,5],[3,6]] | [[4,1],[5,2]] | true |
| 9 | [[0,1],[0,3],[0,7],[8,1],[3,6],[1,2],[4,7],[7,5]] | [[4,1],[8,7],[6,5]] | false |
입출력 예에 대한 설명
입출력 예 #1
동굴 그림은 아래와 같습니다.

방문 순서를 지켜야 하는 방 번호는 다음과 같습니다.
- 6번 → 7번
- 4번 → 1번
- 8번 → 5번
따라서 모든 방을 방문할 수 있는 방법 중 하나는 다음과 같습니다.
- 0번 → 3번 → 6번 → 3번 → 0번 → 7번 → 4번 → 7번 → 0번 → 1번 → 8번 → 1번 → 2번 → 1번 → 0번 → 7번 → 5번
입출력 예 #2

다음 순서로 각 방을 방문하면 됩니다.
- 0번 → 7번 → 4번 → 7번 → 5번 → 7번 → 0번 → 3번 → 6번 → 3번 → 0번 → 1번 → 8번 → 1번 → 2번
입출력 예 #3

규칙에 맞게 모든 방을 방문할 수 있는 방법이 없습니다.
풀이
카카오 2020 인턴십 5번문제 입니다. 정확성과 효율성 두 가지 채점사항이 있습니다.
문제를 푸는데 꽤나 오랜 시간이 걸려서 푼 문제로 다른 사람의 풀이방법이 다 제각각이고 정리가 안되어있어서 혼자서 고민하다가 해결한 문제이다. 단, 푸는 과정에서 "정확성"만 해결한 풀이 방법이 있었고 이를 개선하여서 둘 다 해결한 풀이 방법이 있었다.
정확성만 해결한 풀이방식도 나름대로 맞다고 생각해서 푼 문제이고 이를 개선해나가는 과정을 기록하면 도움이 될 것 같아 먼저 정확성만 해결한 풀이방법부터 설명하고자 한다.(그 다음에 둘다 해결한 풀이도 설명할 것이다.)
정확성 해결 풀이
일단 문제를 보자마자 드는 생각은 무조건 위상정렬이었다. 그냥 프리하게 경로로 진행할 수 있는 동굴이 있는 반면 어떤 동굴을 지나야 지날 수 있는 동굴은 가중치가 생기며 이는 위상정렬이 바로 떠오를 수 밖에 없는 의식의 흐름이다.
정확성 해결 풀이 방식에서는 어떻게 풀었을까? 일단 문제 예제사진을 보자.
지금부터의 설명은 1번 예제를 기준으로 이야기한다.
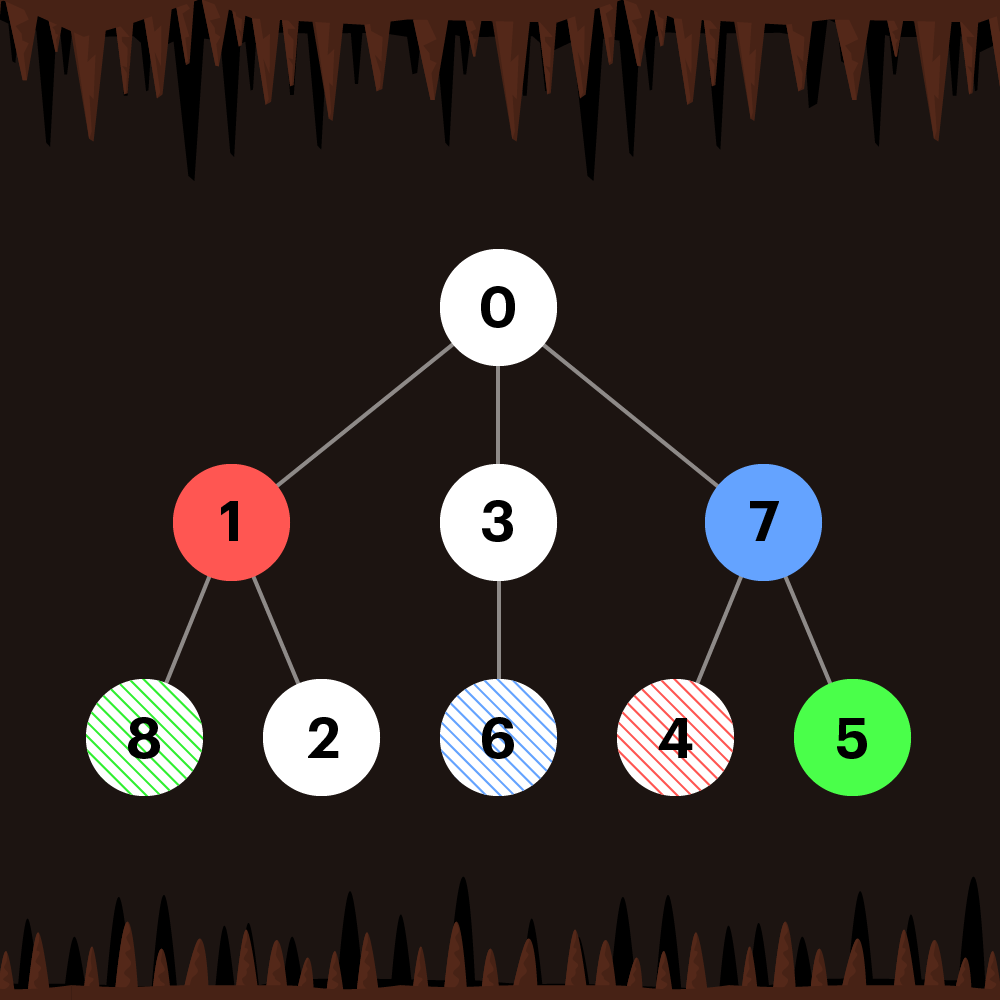
무조건 시작은 0부터 시작해야하며 모든 동굴을 방문했다면 true를 그렇지 못한다면 false를 리턴하면 된다. 단, 1번 예제 사항에서 나와있듯이 order에서 [6,7]이 주어지면 6번동굴을 무조건 통과해야 7번동굴을 통과할 수 있다.
0을 시작점으로 잡게 되면 1, 3, 7로 갈 수 있지만, 1번에서의 제약조건은 5는 8을 통과해야만 갈 수 있고, 7은 6을 통과해야만 갈 수 있고, 1은 4를 통과해야만 갈 수 있다.
따라서 일단 지금 갈 수 있는 경로는 3이다. 0 > 3 > 6은 아무런 제약 조건없이 진행할 수 있다.
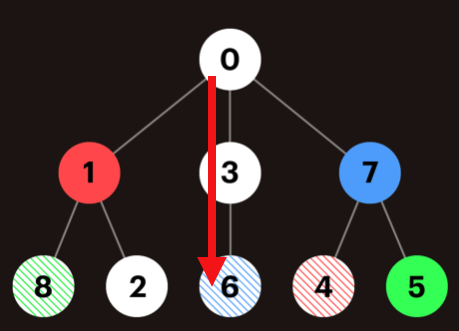
6을 지났으니 이제 열리는 동굴은 7번이 열리기 때문에 7번으로 갈 수 있고, 7번 아래로 또 4를 가면 1번 동굴이 열리고 ...... 이런 방식으로 진행된다. 즉, 문제에서 요구하는 사항은
0 > 3 > 6 > 7 > 4 > 1 > 8,2 > 5
의 순서대로 이동하기를 바라는 것이다.
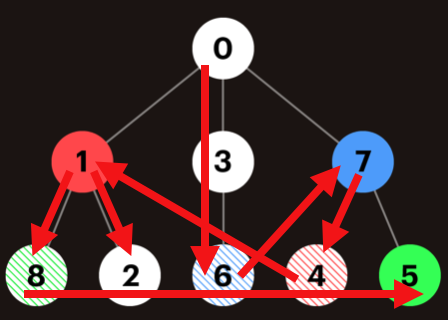
그럼 동굴을 탐험하는 순서를 결정해야하는데 어떻게 동굴을 순차적으로 탐험하고 열린 동굴을 찾아내서 갈 수 있을까?를 고민하는 시점에서 생각의 오류를 범했다.
만약 6을 탐험했다면 7이 열리게 되는 것을 6이 알아챌 수 있고 그럼 일단은 계속 이전값으로 돌아가면 7을 다시 찾을 수 있겠다라는 생각을 하게 됐다. 즉, 위와 같은 방식으로 이동한 것이 아니라
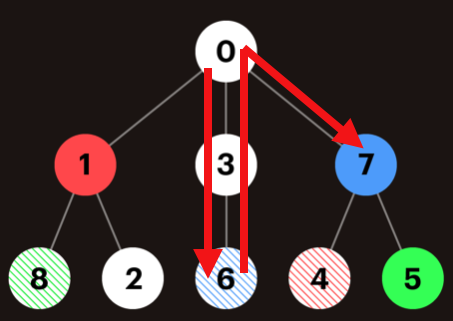
와 같은 방식으로 비효율적인 탐색을 했었다. 지금이야 풀이방법을 제대로 알고 푼 상태이니 진짜 비효율적으로 탐색한다고 생각하지만 당시에는 BFS를 통한 탐색을 할 때 이동하려면 항상 바로 옆에 값으로만 이동해야한다는 사고방식에 갇혀서 경로를 무조건 이전 경로로 가는 것만 생각했다.. 그리고 일단 동굴을 이어주는 경로가 트리로 부모, 자식으로 준게 아니라 랜덤으로 둘을 찝어놓은 것이기 때문에 방향성을 처음에 알기 힘들어서 이전값만 계속 머릿속에 떠올랐던 것도 있다.
이렇게 하면 문제가 무엇이냐. "다" 탐색해야한다. 내가 이전에 왔던 경로로도 탐색을 하는 경우가 발생하게되기 때문에 최악의 경우로 O(n*n)이 되어 n이 최대가 200,000인 이 문제에서는 효율성에서 무조건 터질 수 밖에 없는 구조였던 것이다.
정확성 + 효율성 해결 풀이
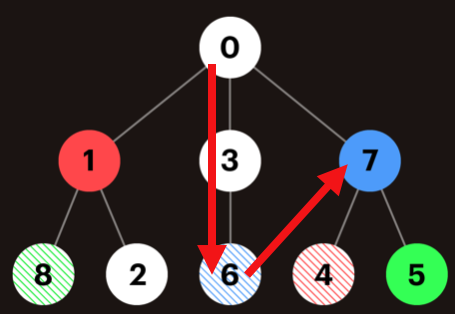
그럼 어떻게 풀어야할까?? 내가 방문한 동굴이 어떤 동굴이 열리는 것에 영향을 끼쳤고 그 동굴의 indegree가 0이 되어 열린다면 그 동굴로 순간이동 해주면 된다. order의 [6,7]을 예로 들어보면 다음 그림과 같다.
for(int i=0; i<link[tmp].size(); i++){
int next = link[tmp].get(i);
indegree[next]--;
if(indegree[next]==0){
queue.add(next);
}
}
link는 어떤 동굴이 열리면 다음 동굴이 열릴 수 있는 제한을 담아둔 배열리스트이다. 만약 tmp가 6이라면 next는 7이 될 것이고 6을 방문했으므로 indegree[7]--가 된다. 이때 indegree[7]이 0이 되었다는 것은 7동굴이 열렸다는 의미로 이를 큐에 담아 방문할 준비를 하는 것이다.
어떻게보면 내가 실제 동굴이었다면 0 > 3 > 6 > 3 > 7로 앞전에 정확성 풀이에서 나온대로 일일히 이동을 해야하지만 효율적으로는 모든 동굴을 탐색해야할 때 불리하기 때문에 6에서 7로 순간이동을 했다고 보면된다.
이렇게 순간이동으로 풀이방식을 바꾼 후로 우리는 가장 중요하게 체크해야할 것이 생겼다.
알고리즘상에서야 순간이동을 한다고치지만 일단 실제 문제는 동굴을 걸어서 이동하는 것이기 때문에 6~7까지 모든 동굴을 걸어야한다. 근데, 중간에 진입하지 못하는 동굴이 생기면..?
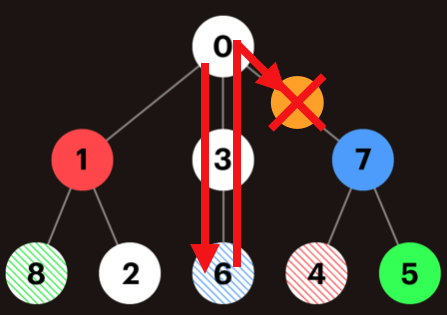
(주황색은 1동굴을 지나야 지날 수 있는 동굴이라 가정한다.)
분명 6이 지났고 7을 제한하는 동굴이 이제 없는데도 "걸어서" 7로 갈 수 있는 길이 없다. 따라서 순간이동을 하게될 때 제한사항을 두어야한다.
제한사항은 동굴이 있을 때 이전에 방문했던 동굴을 체크하는 것이다. 만약 7번 이전에 동굴이 visited하지 않았다면 7번으로 가는 길은 아직 열린상태가 아니기 때문에 접근을 제한한다라고 보면 된다. 이전에 방문한 동굴을 구현하는데는 조금 까다로웠다.
일단 배열 int[] before = new int[n];을 -1로 다 채워놓고 0부터 시작하려했으나 Queue에 0을 넣자마자 0이전값을 검사하는데 에러가 난다. 이전값이 제대로 열려있는지를 검사할 때 0의 이전값은 검사하기가 까다롭다는 것이다. 따라서 어짜피 항상 동굴의 시작은 0부터 한다고 했으니 Queue에 넣는 것은 시작인 0이 아니라 0 다음을 넣으면 되지 않을까 싶었다. 즉, 1 3 7부터 시작하는 것이다.
이렇게 시작하게 되면 어짜피 0으로는 순간이동하지 않으니 0 이전값을 검사할 때 문제가 발생하지 않고, 0을 일단 visited하다고 설정하고 들어갈 것이니 이전 값으로 0을 담아도 크게 문제가 되진 않는다.
if(indegree[0]>0) return false;
Arrays.fill(before, -1);
before[0] = 0;
visited[0] = true;
for(int i=0; i<link[0].size(); i++){
indegree[link[0].get(i)]--;
}
Queue<Integer> queue = new LinkedList<>();
for(int i=0; i<map[0].size(); i++){
int next = map[0].get(i);
before[next] = 0;
queue.add(next);
}
대신, 0을 검토하지 않고 문제에서 0이 제한 동굴에 없다라는 이야기도 없기 때문에 indegree[0]>0하다면 그즉시 false처리를 해준다.(아마 이런 히든 테스트케이스가 이 문제를 판가름하는데 한몫한다고 생각하고 처음부터 문제를 읽지 않고 히든 테케를 생각하지 않은 것에 반성한다..)
while(!queue.isEmpty()){
int tmp = queue.poll();
if(indegree[tmp]>0) continue;
if(before[tmp]==-1 || !visited[before[tmp]]) continue;
if(!visited[tmp]){
visited[tmp] = true;
for(int i=0; i<link[tmp].size(); i++){
int next = link[tmp].get(i);
indegree[next]--;
if(indegree[next]==0){
queue.add(next);
}
}
for(int i=0; i<map[tmp].size(); i++){
int next = map[tmp].get(i);
if(before[tmp] == next) continue;
before[next] = tmp;
if(!visited[next] && indegree[next]==0){
queue.add(next);
}
}
}
}
그후로는 지금까지 이야기했던 순간이동과 이전 동굴이 열렸는지에 대한 내용을 위상정렬을 섞어서 넣은 BFS와 다름없다. 들어온 값이 제한이 있는지 검사하고 이전 경로가 열려있는지 확인한다. 그리고 지금 동굴에 제한된 동굴들을 1씩 내려주면서 만약 그 동굴을 들어갈 수 있게 된다면(indegree==0) Queue에 넣어준다. 이 Queue에 넣는 과정이 결국 순간이동이다.
그리고 연결된 동굴들을 내려가면서 다음 동굴이 지금 동굴을 지나가는 것이므로 이전동굴에 대한 내용을 저장해주고, 지금 동굴의 이전동굴의 경우에는 Queue에 넣지 않고 경로를 이동한다.
결국 이 문제에서 제일 중요했던 것은 위상정렬을 사용하고, 만약 indegree가 0이 되었을 때 해당 값으로 이동하지만 이전 경로가 열려있는지를 확인할 수 있느냐 아니냐였다고 생각한다. (물론 엣지케이스가 틀리기 쉽게 해두어서 채점을 알지 못했다면 그냥 제출하고 말았을 코테로 남았을수도 있다..)
위상정렬을 좀 더 익숙하게 사용할줄 알면 쉽게 풀었을 문제라고 생각한다.
정답 코드
import java.util.*;
class Solution {
public int[] indegree;
public boolean[] visited;
public int[] before;
public ArrayList<Integer>[] map;
public ArrayList<Integer>[] link;
public boolean solution(int n, int[][] path, int[][] order) {
indegree = new int[n];
visited = new boolean[n];
before = new int[n];
map = new ArrayList[n];
link = new ArrayList[n];
for(int i=0; i<n; i++){
map[i] = new ArrayList<>();
link[i] = new ArrayList<>();
}
for(int i=0; i<path.length; i++){
map[path[i][0]].add(path[i][1]);
map[path[i][1]].add(path[i][0]);
}
for(int i=0; i<order.length; i++){
link[order[i][0]].add(order[i][1]);
indegree[order[i][1]]++;
}
if(indegree[0]>0) return false;
Arrays.fill(before, -1);
before[0] = 0;
visited[0] = true;
for(int i=0; i<link[0].size(); i++){
indegree[link[0].get(i)]--;
}
Queue<Integer> queue = new LinkedList<>();
for(int i=0; i<map[0].size(); i++){
int next = map[0].get(i);
before[next] = 0;
queue.add(next);
}
while(!queue.isEmpty()){
int tmp = queue.poll();
if(indegree[tmp]>0) continue;
if(before[tmp]==-1 || !visited[before[tmp]]) continue;
if(!visited[tmp]){
visited[tmp] = true;
for(int i=0; i<link[tmp].size(); i++){
int next = link[tmp].get(i);
indegree[next]--;
if(indegree[next]==0){
queue.add(next);
}
}
for(int i=0; i<map[tmp].size(); i++){
int next = map[tmp].get(i);
if(before[tmp] == next) continue;
before[next] = tmp;
if(!visited[next] && indegree[next]==0){
queue.add(next);
}
}
}
}
for(int i=0; i<n; i++){
if(!visited[i]) return false;
}
return true;
}
}