[프로그래머스/JAVA] 모두 0으로 만들기
문제 설명
각 점에 가중치가 부여된 트리가 주어집니다. 당신은 다음 연산을 통하여, 이 트리의 모든 점들의 가중치를 0으로 만들고자 합니다.
- 임의의 연결된 두 점을 골라서 한쪽은 1 증가시키고, 다른 한쪽은 1 감소시킵니다.
하지만, 모든 트리가 위의 행동을 통하여 모든 점들의 가중치를 0으로 만들 수 있는 것은 아닙니다. 당신은 주어진 트리에 대해서 해당 사항이 가능한지 판별하고, 만약 가능하다면 최소한의 행동을 통하여 모든 점들의 가중치를 0으로 만들고자 합니다.
트리의 각 점의 가중치를 의미하는 1차원 정수 배열 a와 트리의 간선 정보를 의미하는 edges가 매개변수로 주어집니다. 주어진 행동을 통해 트리의 모든 점들의 가중치를 0으로 만드는 것이 불가능하다면 -1을, 가능하다면 최소 몇 번만에 가능한지를 찾아 return 하도록 solution 함수를 완성해주세요. (만약 처음부터 트리의 모든 정점의 가중치가 0이라면, 0을 return 해야 합니다.)
제한사항
- a의 길이는 2 이상 300,000 이하입니다.
- a의 모든 수는 각각 -1,000,000 이상 1,000,000 이하입니다.
a[i]는 i번 정점의 가중치를 의미합니다.
- edges의 행의 개수는 (a의 길이 - 1)입니다.
- edges의 각 행은
[u, v]2개의 정수로 이루어져 있으며, 이는 u번 정점과 v번 정점이 간선으로 연결되어 있음을 의미합니다. - edges가 나타내는 그래프는 항상 트리로 주어집니다.
- edges의 각 행은
입출력 예
| a | edges | result |
|---|---|---|
[-5,0,2,1,2] |
[[0,1],[3,4],[2,3],[0,3]] |
9 |
[0,1,0] |
[[0,1],[1,2]] |
-1 |
입출력 예 설명
입출력 예 #1
- 다음 그림은 주어진 트리의 모든 정점의 가중치를 0으로 만드는 과정을 나타낸 것입니다.

- 2번 정점과 3번 정점을 선택하여 2번 정점은 1 감소시키고, 3번 정점은 1 증가시킵니다. (2번 반복)
- 3번 정점과 4번 정점을 선택하여 4번 정점은 1 감소시키고, 3번 정점은 1 증가시킵니다. (2번 반복)
- 0번 정점과 3번 정점을 선택하여 3번 정점은 1 감소시키고, 0번 정점은 1 증가시킵니다. (5번 반복)
- 모든 정점의 가중치를 0으로 만드는 데 필요한 최소 행동 횟수는 9번이므로, 9를 return 해야 합니다.
입출력 예 #2
- 주어진 트리는 모든 정점의 가중치를 0으로 만드는 것이 불가능하므로, -1을 return 해야 합니다.
풀이
프로그래머스 월드 코드 챌린지 시즌2에서 3번으로 나온 문제이다.
BFS, DFS 풀이 방법은 여러가지가 있지만 개인적으로 Tree 문제를 풀 때 BFS로 푸는 것을 선호하여서 BFS 풀이방법을 설명하고자 한다.
문제의 정점을 탐색해서 answer를 도출해내기 앞서서 먼저 처리해야할 부분이 있다. "전부 더해서 0이 되는가 안되는가". 일단 Node들에서 완전히 새로운 값들을 생성해내서 0으로 만드는 것이 아니라 각각의 Node가 가진 값들을 옮기면서 0으로 만들어야한다. 따라서 먼저 모든 Node를 더해보고 0이 되는지 안되는지를 확인해야한다.
또한 이 과정에서 배열을 long 배열로 옮기는 작업을 했다. 차후에 배열을 Node 값을 저장하는 용도로 사용하게될 것인데 각 값이 1,000,000가 최대이기 때문에 만약에 int 배열을 그대로 사용한다면 범위를 초과한다.
n = atmp.length;
a = new long[n];
for(int i=0; i<n; i++){
a[i] = atmp[i];
answer += a[i];
}
if(answer!=0) return -1;
이후엔 Node가 단 두개인 경우를 생각한다. Node가 두 개면? 하나만 옮기면 된다. 따라서 한쪽 Node를 절대값 처리한 후 return 한다.
if(n==2) return Math.abs(a[0]);
이때부터는 풀이 방식이 두 가지로 나뉘었었다. root를 기점으로 leaf로 내려가면서 DFS를 사용할 것인지, leaf부터 올라가면서 BFS를 사용할 것인지 였다. 이미 BFS를 사용하기로 했고 처음 떠오른 방식이 leaf부터 올라가는 방식이었기 때문에 해당 방식을 사용했다.
그럼 leaf와 root를 구하는 조건은?
일단 leaf는 연결된 Node가 단 1개면 되며 root는 아무거나 하나의 Node로 잡아도 상관없다. 어짜피 구조는 Tree 구조이며 root에 대한 어떠한 제한 조건도 걸려있지 않기 때문에 무슨 Node를 root로 잡건 root 아래로 뿌리내려지는 Tree 구조를 만들 수 있다.
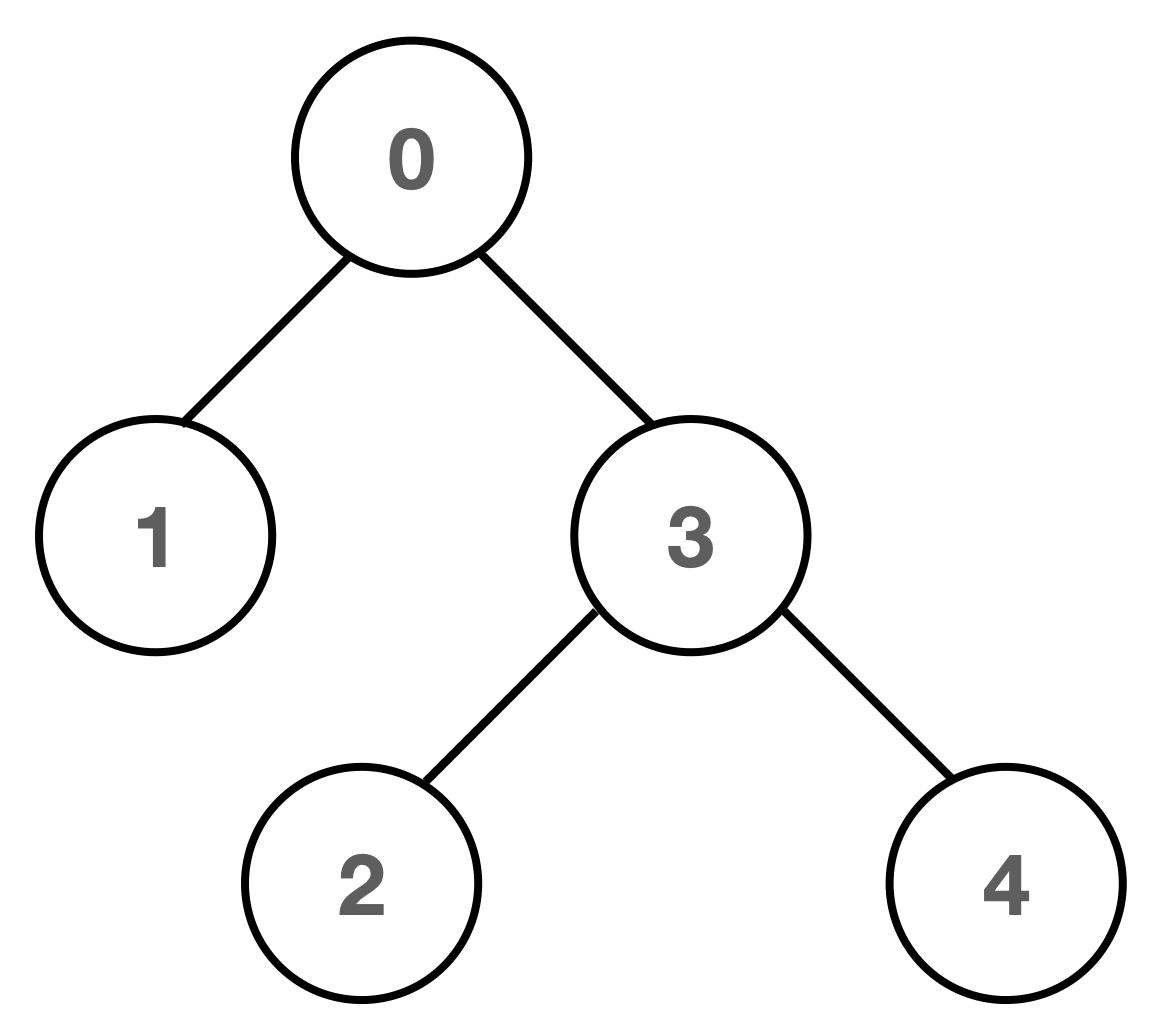
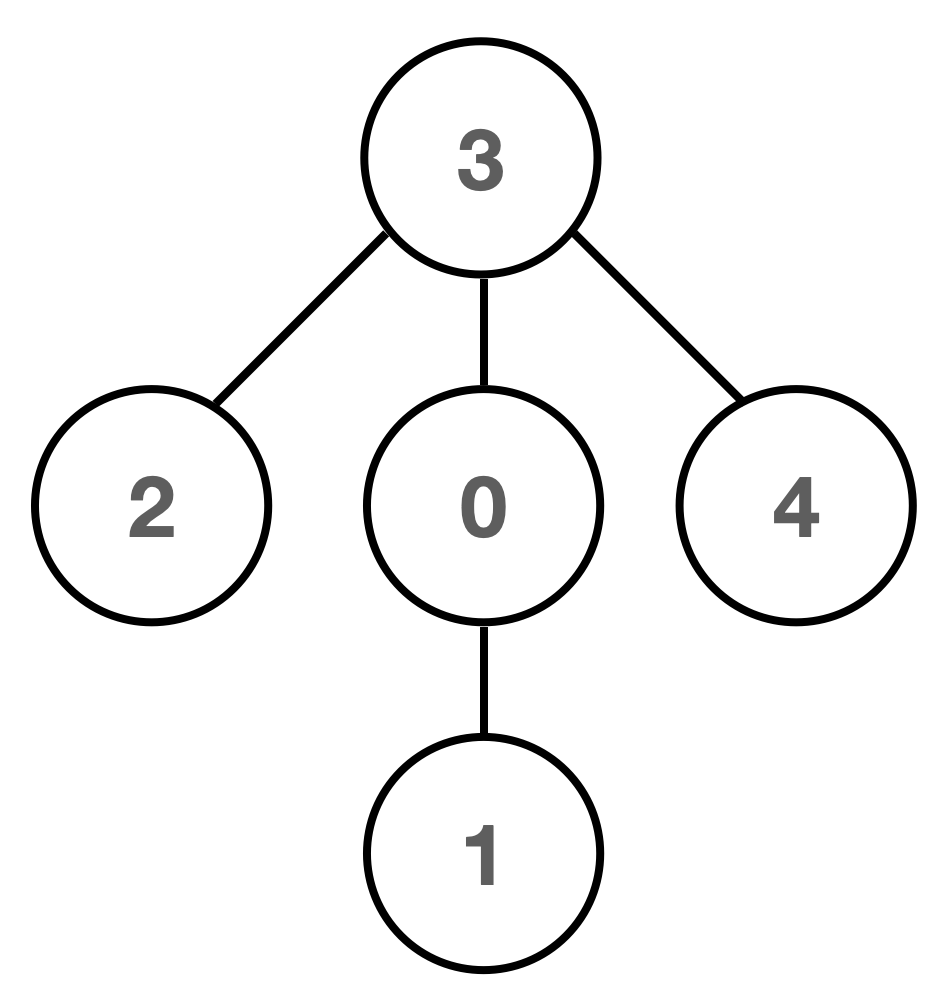
0을 root로 만들거나, 3을 root로 만들거나 결국 input으로 주어진 edges가 부모, 자식 관계를 나타낸 것이 아닌 그냥 임의의 노드끼리의 간선을 나타낸 것이기 때문에 내가 어떤 Node를 root로 잡건 내가 잡는 root가 그 Tree의 root가 되어 사용할 수 있게 된다.
leaf는 물론 항상 Tree의 자식이 없는 Node이기 때문에 root를 제외한 간선 연결이 하나만 된 Node를 leaf라고 정의한다.
map = new ArrayList[n];
for(int i=0; i<n; i++){
map[i] = new ArrayList<>();
}
indegree = new int[n];
for(int i=0; i<edges.length; i++){
map[edges[i][0]].add(edges[i][1]);
map[edges[i][1]].add(edges[i][0]);
indegree[edges[i][0]]++;
indegree[edges[i][1]]++;
}
Queue<Integer> queue = new LinkedList<>();
for(int i=1; i<n; i++){
if(map[i].size()==1) queue.add(i);
}
일단 input으로 주어진 edges들을 가지고 모든 Node들에게 간선에 대한 정보를 다 입력한 상태이다. 이때 indegree는 차후 leaf부터 시작하여 root에게 가기까지 부모 Node로 올라가도되는지 안되는지를 판단하는 지표가 되기 때문에 가중치를 미리 계산해 두었다.
이 풀이에서는 root를 항상 0으로 두었다. 별다른 이유는 없고 leaf를 따로 추가하는데 코드가 깔끔했기 때문이다. leaf는 해당 node의 간선 size가 1일 때 queue에 넣었고 1부터 시작한다면 leaf가 0인 경우를 따로 if문으로 빼지않아도되기 때문에 root를 0으로 취한 것이다.
따라서 지금부터의 풀이는 root를 0을 두고 풀이하기 때문에 아래 그림을 통해서 설명할 예정이다.

while(!queue.isEmpty()){
int tmp = queue.poll();
answer += Math.abs(a[tmp]);
indegree[tmp]--;
for(int i=0; i<map[tmp].size(); i++){
int next = map[tmp].get(i);
if(indegree[next]==0) continue;
indegree[next]--;
a[next] += a[tmp];
if(indegree[next]==1){
if(next == root) continue;
queue.add(next);
}
}
}
메인 부분인 leaf부터 root까지 값을 올려주면서 계산하는 로직이다.
사실 조금더 간편하게 remove() 메소드를 이용해서 올라갈때마다 자식에 대한 관계를 끊어서 손쉽게 root를 찾는 방법도 있었지만 문제의 오류인지 문제가 요구하는 바가 아닌지 알 수 없는 오류로 시간초과가 나서 해당 방법은 사용하지 못했다.(로직은 정답풀이와 100% 일치하기 때문에 해당 방법 또한 문제가 없어보인다.)
일단 queue에 들어가는 Node는 "항상" leaf인 Node를 넣어주었다. 따라서 해당 leaf를 받았을 때 먼저 이를 위로 옮긴다는 생각을 하고 answer에 절댓값을 더해주었다. 그리고 indegree 가중치를 1을 제거하면서 해당 Node를 사용했다는 표시를 해줬다. 설령 그림에서 3 Node를 받았더라도 3 Node의 간선이 0, 2, 4를 가르키지만 2와 4는 indegree 가중치를 제거했기 때문에 무조건 0일것이므로 탐색하지 않는 방식이다.
4부터 들어갔다고 가정했을 때 4의 간선은 3 뿐이다. 따라서 3을 next로 받고 3의 indegree 가중치를 -1 해주면서 4에 있던 값을 3으로 옮겨준다. 단, 아직 3에게 남아있는 간선은 0으로가는 1개가 아닌 2까지 합쳐서 총 2개의 간선이 있기 때문에 이동하지는 않는다.
4가 지난 후 2가 지났을 때 그제서야 3에게 남는 간선은 0이기 때문에 queue에 포함해주며, 3도 지금까지와 마찬가지로 answer에 절댓값을 더해주며 끝이난다.
결국 해당 문제의 주요 요점은 Tree구조에서 leaf와 root를 어떻게 찾을것이며, leaf부터 root까지 올라가면서 어떻게 부모 Node만 찾아서 올라갈 것이냐이다.
remove()메소드를 썼다고 시간초과나는 건 이해가 안간다... LinkedList를 썼는데도 불구하고 시간초과가나서 포기했다)
정답 코드
import java.util.*;
class Solution {
public long[] a;
public int n;
public long answer = 0;
public ArrayList<Integer>[] map;
public int[] indegree;
public int root = 0;
public long solution(int[] atmp, int[][] edges) {
n = atmp.length;
a = new long[n];
for(int i=0; i<n; i++){
a[i] = atmp[i];
answer += a[i];
}
if(answer!=0) return -1;
if(n==2) return Math.abs(a[0]);
map = new ArrayList[n];
for(int i=0; i<n; i++){
map[i] = new ArrayList<>();
}
indegree = new int[n];
for(int i=0; i<edges.length; i++){
map[edges[i][0]].add(edges[i][1]);
map[edges[i][1]].add(edges[i][0]);
indegree[edges[i][0]]++;
indegree[edges[i][1]]++;
}
Queue<Integer> queue = new LinkedList<>();
for(int i=1; i<n; i++){
if(map[i].size()==1) queue.add(i);
}
while(!queue.isEmpty()){
int tmp = queue.poll();
answer += Math.abs(a[tmp]);
indegree[tmp]--;
for(int i=0; i<map[tmp].size(); i++){
int next = map[tmp].get(i);
if(indegree[next]==0) continue;
indegree[next]--;
a[next] += a[tmp];
if(indegree[next]==1){
if(next == root) continue;
queue.add(next);
}
}
}
return answer;
}
}